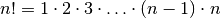different permutations of the numbers from 0 to 
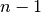. Since we only care about permutations that start with 0, to solve an 
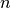-city TSP instance with brute force requires that we look at exactly 
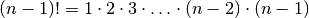different permutations.The traveling salesman problem, referred to as the TSP, is one of the most famous problems in all of computer science. It’s a problem that’s easy to describe, yet fiendishly difficult to solve. In fact, it remains an open question as to whether or not it is possible to efficiently solve all TSP instances.
Here is the problem. Suppose you are a salesman travelling that has a list of cities that you want to visit. You want to go to each city exactly once. Naturally, you want to tour all the cities in the order that requires traveling the shortest distance.
For instance, suppose you’re visiting these four cities:
0 1 2 3
You always start, and end, at 0, your home city. We assume the following distances between cities:
dist(0, 1) = 10
dist(0, 2) = 10
dist(0, 3) = 14
dist(1, 2) = 14
dist(1, 3) = 10
dist(2, 3) = 10
In this case the distances are symmetric, i.e. dist(a, b) is always the same as dist(b, a). So for example we know dist(3, 2) = 10 because we are told dist(2, 3) = 10.
Here are some different tours of the cities:
0 to 1 to 3 to 2 (and back to 0); total distance = 10 + 10 + 10 + 10 = 40 0 to 2 to 3 to 1 (and back to 0); total distance = 10 + 10 + 10 + 10 = 40 0 to 3 to 1 to 2 (and back to 0); total distance = 14 + 10 + 14 10 = 48 0 to 2 to 1 to 3 (and back to 0); total distance = 10 + 14 + 10 + 14 = 48Clearly, some tours are shorter than others. For this small 4-city example it is easy to see that the shortest way to visit all the cities is to go around the edges and avoid the long diagonals.
But not all instances of the TSP are so simple or so small. For instance, suppose you want to visit all 4600-plus Canadian cities. It is not at all obvious how you should go about finding the shortest possible tour of so many cities.
If you think about it, representing a TSP tour is not too hard: it is just a permutation of the cities, with the added restriction that the first city must always be 0 (your home city). For instance, we can write the above tours compactly like this:
0, 2, 3, 2
0, 2, 3, 1
0, 3, 1, 2
0, 2, 1, 3
Once we realize a tour is a permutation, then a brute-force algorithm that is guaranteed to always solve the TSP becomes evident:
Brute-force algorithm: Examine all possible permutations of cities, and keep the one that is shortest.
It turns out that there are exactly 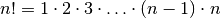different permutations of the numbers from 0 to 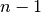. Since we only care about permutations that start with 0, to solve an 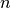-city TSP instance with brute force requires that we look at exactly 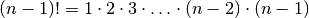different permutations.
Lets give some thought to the overall structure and organization of our program.
First, we will assume that the cities are named 0 to n - 1, and that a tour of these n cities is a permutation of the numbers from 0 to n - 1. We assume that 0 is the home city, and that all tours start with 0.
Second, we need some way to store the cities. Since our cities are on a 2-dimensional map, we can store them as (x, y) points using the Point class from previous notes. We’ll store the cities as a vector , where each city’s name is the same as its index number in the vector , i.e. the city at index location 0 is named 0, the city at index location 1 is named 1, and so on.
We’re also going to need a function to calculate the distance between two cities, and another function to calculate the total length of a tour of cities. So lets write a class called Tsp_map whose responsibility is to take care of such details. A Tsp_map object will store a collection of cities, provide functions for calculating distances, and maybe some other helper functions as well.
Recall from math class that distance between the points (x, y) and (a, b) is given by this formula:
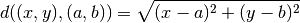
Third, lets agree to represent a tour (i.e. a permutation of city names) as a vector . The numbers in it represent the names of the cities in a particular Tsp_map , and the order of the numbers is the order in which the cities will be visited.
Using the above notes as a guide, lets start to write the Tsp_map class:
#include "Point.h" class Tsp_map private: vectorPoint> cities; public: // add a city at point p void add(const Point& p) cities.push_back(p); > // add a city at (x, y) void add(double x, double y) Point p(x, y); add(p); > // # of cities int size() const return cities.size(); > // calculate the distance between cities i and j double dist_between(int i, int j) const return dist(cities[i], cities[j]); // dist is from Point.h > // calculate the score of the given tour double score(const vectorint>& tour) const double result = dist_between(tour[0], tour[size() - 1]); for(int i = 1; i size(); ++i) // i starts at 1, not 0! result += dist_between(tour[i - 1], tour[i]); > return result; > // return a starting tour of all the cities in the order 0, 1, 2, 3, // . vectorint> get_default_tour() const vectorint> tour(size()); for(int i = 0; i size(); ++i) tour[i] = i; > return tour; > >; // class Tsp_map
Note the following:
We can use a Tsp_map like this:
Tsp_map cities; cities.add(0, 0); cities.add(10, 0); cities.add(0, 10); cities.add(10, 10); // get a starting tour vectorint> tour(cities.get_default_tour()); // .
Our tours are represented as plain vector objects. A problem with this is that writing vector all the time is a bit tedious, and it also doesn’t clearly indicate that it is being used to represent a tour. So we what we can do is to use typedef to create a synonym for vector with a more descriptive name:
typedef vectorint> Tour; // Tour is a synonym for vector // .
Now we can write Tour instead of vector :
// get a starting tour Tour tour(cities.get_default_tour());
This makes the purpose of the code clearer, and clearer code is always a good thing.
Now lets write a function that uses brute force to solve a TSP problem. The header will look like this:
void brute_force(const Tsp_map& cities) // . >
This is not inside the Tsp_map function. Instead, it is a stand-alone function that takes a Tsp_map as input.
In pseudocode, the brute force algorithm goes like this:
As is often done in pseudocode, we use an arrow “⇦” to indicate variable assignment. The reason for this is that it is more suggestive than “=”, plus it lets us use “=” in the usual mathematical way in pseudocode if we need it.
The next step is to convert the pseudocode to C++:
void brute_force_solver(const Tsp_map& cities) Tour tour(cities.get_default_tour()); double best_score = cities.score(tour); Tour best_tour(tour); cout <tour <" score = " <best_score <endl; while (next_permutation(tour.begin() + 1, tour.end())) double s = cities.score(tour); if (s best_score) best_score = s; best_tour = tour; > cout <tour <" score = " <s <endl; > // while cout <"best tour: " <best_tour <"\nscore = " <best_score <endl; >
The most interesting detail here is how the permutations are generated. It turns out that the C++ standard template library (the STL) has a function called next_permutation that will re-arrange the elements of a sequence to the next permutation in lexicographic order.
Lexicographic order is a generalization of alphabetical order that works with numbers. By starting with the permutation 0, 1, 2, . n - 1, next_permutation guarantees to cycle through all possible permutations, returning false when it as the last one.
Notice that we pass in tour.begin() + 1 instead of tour.begin() :
while (next_permutation(tour.begin() + 1, tour.end())) // .
That’s because we know, from our definition of the problem, that the first element of a tour should always be 0. Thus we only need to permute the n - 1 numbers after 0.
Solving the TSP by brute force has a couple of important benefits:
For small number of cities the brute-force solver works well. For example:
int main() Tsp_map cities; cities.add(0, 0); cities.add(10, 0); cities.add(0, 10); cities.add(10, 10); cities.add(4, 5); cities.add(7, 1); cities.add(9, 2); cities.add(5, 0); cities.add(6, 1); cities.add(5, 5); cities.add(0, 5); brute_force_solver(cities); >
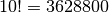
This 11-city problem checks in about 3.6 seconds on my computer. Adding one more city causes it to run in about 44 seconds, which is close to what you would expect given that it is checking 11 times as many permutations.
As you can see from these two examples, the big problem solving the TSP by brute force is that it’s incredibly slow. To solve an n-city TSP problem requires generating exactly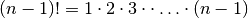 
permutations. For even smallish values of , 
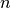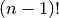turns out to be huge. For example:
n n! ----- 0 1 1 1 2 2 3 6 4 24 5 120 6 720 7 5040 8 40320 9 362880 10 3628800 11 39916800 12 479001600 13 6227020800 14 87178291200 15 1307674368000 16 20922789888000 17 355687428096000 18 6402373705728000 19 121645100408832000 20 2432902008176640000
As n get bigger,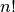 
grows worse than exponentially. If you want to use brute-force to solve a 20-city problem, then you’ll need to generate 121645100408832000 different permutations, i.e. over 120 quintillion permutations. But that’s nothing compared to the 
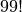different permutations you would need to search through for a 100-city problem:
933262154439441526816992388562667004907159682643816214685929638\ 952175999932299156089414639761565182862536979208272237582511852\ 109168640000000000000000000000
In practice, no matter how fast your computer, or how many you have, you won’t be able to generate this many permutations in a reasonable amount of time.
If generating all permutations is too slow in practice, then lets try another extreme: generating permutations at random.
Random Tour Algorithm: Generate random tours, and save the shortest one. Stop when you have no more time left to search for tours.
The code for this algorithm is very similar to the code for generating all permutations:
void random_guesser(const Tsp_map& cities, int num_guesses = 1000000) Tour tour(cities.get_default_tour()); double best_score = cities.score(tour); Tour best_tour(tour); for(int i = 0; i num_guesses; ++i) random_shuffle(tour.begin() + 1, tour.end()); double s = cities.score(tour); if (s best_score) best_score = s; best_tour = tour; > > cout <"best tour: " <best_tour <"\nscore = " <best_score <endl; >
As with the brute-force solver, we use best_score and best_tour to keep track of the shortest tour seen so far. Each time through the for-loop, the tour cities are shuffled using the standard random_shuffle algorithm, and then scored. If this shuffled tour is shorter than the shortest one seen so far, it’s saved.
It’s up to the programmer to decided how many random guesses should be made. By default, a million random guesses are made, which runs in a couple of seconds on my computer.
However, for large TSP problems random guessing is terrible because it blindly takes permutations from a huge search space. It’s like searching for a needle in a giant haystack by randomly plucking out one straw at a time.
As mentioned, the TSP is an extremely well-studied problem, and numerous fast algorithms that usually find pretty short (not always the shortest) tour have been created. As just one example of a better method, consider this algorithm for constructing a tour a city at a time:
While this algorithm does not guarantee to always find a shortest possible tour, it is certainly better than random guessing, and fast enough to be applied to very large TSP instances.
It’s currently unknown if there is an algorithm that can always guarantee to efficiently find the shortest tour in any TSP. The majority of computer scientists probably believe that there is no such algorithm, but this has not been proved.
If you’d like to learn more about the TSP and how to solve it efficiently, a good starting place is this TSP page. One of the many interesting things on that page is an optimal tour of all of Canada’s 4,663 main cities.
Brute force doesn’t work well for the TSP, but for some problems it is a good solution method. For example, perhaps you have heard of “alphametic”, or “cryptarithm” puzzles like this:
S E N D + M O R E --------- M O N E Y
Each letter of the puzzle stands for a single digit, and different letters must have different values. Also, letters at the start of a word can’t be 0.
A brute force solution to this puzzle work like this:
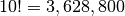
Here’s a program that solves the puzzle:
#include "std_lib_cmpt125.h" // 0 1 2 3 4 5 6 7 // Variables: S, E, N, D, M, O, R, Y // S and M not 0 void check(const vectorint>& v) int send = 1000 * v[0] + 100 * v[1] + 10 * v[2] + v[3]; int more = 1000 * v[4] + 100 * v[5] + 10 * v[6] + v[1]; int money = 10000 * v[4] + 1000 * v[5] + 100 * v[2] + 10 * v[1] + v[7]; if (send + more == money && v[0] != 0 && v[4] != 0) cout <"Solution found: "; for(int i = 0; i v.size(); ++i) cout <v[i] <" "; > cout <endl; > > int main() cout <"The SEND + MORE = MONEY Puzzle\n\n"; vectorint> vars(10); // initialize to 0, 1, 2, . 9 for(int i = 0; i 10; ++i) vars[i] = i; > int count = 0; check(vars); while (next_permutation(vars.begin(), vars.end())) check(vars); ++count; > cout <"Permutations checked: " <count <endl; > // main
On my computer, this program takes 0.08 seconds to find two solutions:
Solution found: 9 5 6 7 1 0 8 2 3 4 Solution found: 9 5 6 7 1 0 8 2 4 3
These are actually the same solution since we only care about the first 8 digits; the last 2 are not used in this puzzle:
9 5 6 7 + 1 0 8 5 --------- 1 0 6 5 2
